- Q
-
Minitab 18 - Definitive Screening Designs 和一般傳統的因子設計有何不同?
- A
-
Definitive Screening Designs
什麼是 Definitive Screening Design?
Definitive Screening Design 是解析度 (resolution) IV 設計。在解析度 IV 設計中,主效應與 2 因子交互作用不互為別名 (aliased)。在 Definitive Screening Design 中,2 因子交互作用通常彼此或與平方項部分交絡 (confounded),但您仍可以估計某些 2 因子交互作用。平方項不與主效應項互為別名,因此您可以估計某些平方項。在許多情況下,我們可以估計在試驗中涉及到任何 3 因子的所有 2 因子交互作用項和平方項。有關別名的更多資訊,請至 什麼是交絡和別名結構?。
Definitive Screening Design與解析度III篩選設計不同處?
Definitive Screening Design 是一種解析度 IV 設計。在解析度 IV 設計中,主效應不與 2 因子交互作用互為別名。與更複雜的設計相比較時,解析度 III 設計具有相對較少的試驗數,因此解析度 III 設計是常見的篩選設計。但是,在解析度 III 設計中,主效應與 2 因子交互作用互為別名。
當您希望使用額外的試驗,以便主效應不與 2 因子交互作用互為別名時,請考慮 Definitive Screening Design。要建立一個 Definitive Screening Design,請使用 Stat > DOE > Screening > Create Screening Design。當您希望假設 2 因子交互作用可以在篩選期間忽略時,請考慮解析度 III 設計。要建立解析度 III 設計,請使用 Stat > DOE > Factorial > Create Factorial Design 並選擇 Plackett-Burman 設計或 2 水準因子設計。
Definitive Screening Design 與 2 水準設計有何不同?
Definitive Screening Design 包含 2 水準設計中所沒有的試驗,因此您可以使用 Definitive Screening Design 來估計平方項。平方項說明反應結果中的曲率。曲線關係的一個範例是土壤中的氮含量和植物所結的水果數量。如果增加正確數量的氮,水果產量會增加,但是,如果增加太多的氮,則反而降低水果產量。在 Definitive Screening Design 中,任何平方項都不與主效應項互為別名。
除了 Definitive Screening Design 外,還有兩個常見的篩選設計類型:Plackett-Burman 設計和解析度 III 部分因子設計。Plackett-Burman 設計和解析度 III 部分因子設計皆是 2 水準設計。您無法根據 2 水準設計來估計任何平方項。
Plackett-Burman 設計和部分因子設計可以包括中心點。但是,增加中心點到這些設計中會使所有的二次效應互為別名。您可以根據具有中心點的設計評估至少 1 個因子的效應是否與反應結果具有曲線關係。但是,您無法相互區分任何平方項。
當希望使用額外的試驗在篩選實驗中包含平方項時,請考慮 Definitive Screening Design。要建立 Definitive Screening Design,請使用 Stat > DOE > Screening > Create Screening Design。在使用試驗估計平方項之前,可考慮使用 2 水準設計來評估任何平方項是否重要。要建立 2 水準設計,請使用 Stat > DOE > Factorial > Create Factorial Design。
Definitive Screening Design的範例
工程師正在開發一種新型超音波清洗機。工程師使用篩選設計確定哪些潛在因子影響清洗機的輸出功率。
該研究包括以下 7 個因子。
A. 培訓時間 (秒):調幅的持續時間
B. Degas 時間 (秒):調製之間的氣泡釋放休息時間
C. 猝發時間 (毫秒):高能氣泡的猝發時間
D. 安靜時間 (毫秒):清洗機的休息時間
E. 中心 (千赫):遠離 40 千赫的中心頻率
F. 頻寬 (千赫):從中心頻率掃描的差值
G. 掃描時間 (秒):完成 1 次掃描所需的時間
工程師考慮使用解析度 III 部分因子設計和 Definitive Screening Design,因為他們希望一個充分適當的模型可以擁有 1 個或多個因子的平方項。在解析度 III 部分因子設計中,一個具有 3 個中心點的一次重覆設計中只有 11 個試驗數。但是,如果工程師需要通過增加軸點試驗來估計平方項,則解析度 III 部分因子設計會增大到 25 個試驗數。工程師決定使用可以借助於 17 個試驗來估計平方項的 Definitive Screening Design。
在試驗之後,一個工程師分析 Definitive Screening Design 以確定最重要的效應。該工程師從一個具有主效應的模型查看標準化效應的 Pareto 圖。該圖還包括模型中沒有的效應。在 Pareto 圖中,A 和 D 是最重要的因子。其他任何因子都不具有大的主效應。
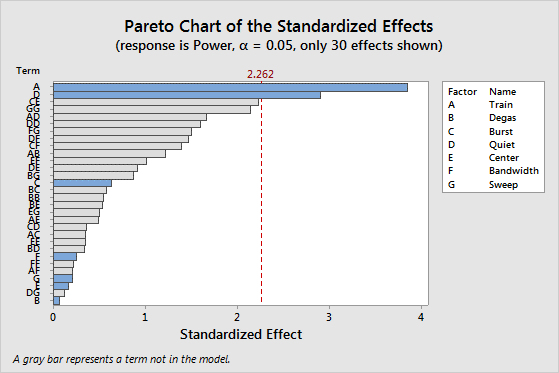
由於 B 是 Pareto 圖上最小的模型項,因此該工程師將 B 從模型中排除。工程師查看模型中沒有 B 時的 Pareto 圖。在第二個 Pareto 圖中,該工程師注意到 2 因子交互作用 (CE) 和平方項 (GG) 的效應超越輔助線,儘管這些項不在模型中也是如此。
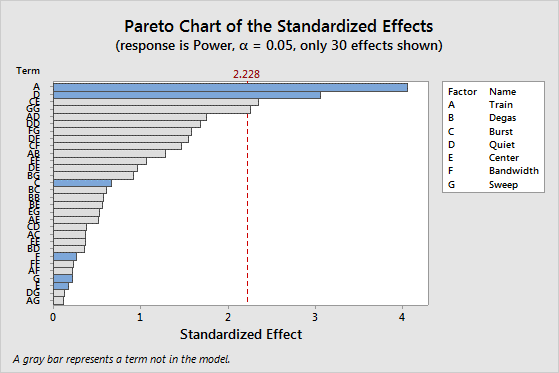
該工程師進一步細化此模型並發現,當模型中包括 CE 交互作用和 GG 平方項時,這些項仍具有統計顯著性。該工程師確定因子 B 和 F 沒有大的主效應而且不可能位於任何大的 2 因子交互作用中。該工程師確定篩選試驗的結果是,為了更好地瞭解該過程,在進一步的試驗中可以排除因子 B 和 F。