- Q
-
Minitab 18 - 我如何解釋非常態容忍區間 (Nonnormal Tolerance Interval)?
- A
-
容忍區間 (非常態分配) 的主要結果
請完成以下步驟來解釋容忍區間 (tolerance intervals)。
步驟 1:評估資料的合適分配
Minitab 為使用分配的方法和非參數方法提供容忍區間。如果您能夠可靠地假設資料服從某分佈,則採用的容忍區間可以是使用該分佈的方法的區間。相反地,如果您不能可靠地假設資料服從某分佈,則必須嘗試其他分佈或者使用非參數方法的容忍區間。
要確定您能否假設資料服從某分佈,請比較 Anderson-Darling 檢定的 p 值與顯著性水準 (α)。顯著水準 0.05 表示當資料實際上服從某分佈時,判定資料不服從該分佈的風險為 5%。
P 值 ≤ α:資料不服從該分佈 (拒絕 H0)
如果 p 值小於或等於顯著水準,則可以得出資料不服從該分佈的結論。在這種情況下,您必須嘗試其他分佈或者使用非參數方法的容忍區間。
P 值 > α:證據不足,無法得出資料不服從該分佈的結論 (無法否定 H0)
如果 p 值大於顯著水準,則您沒有足夠證據得到資料不服從某分佈的結論。在這種情況下,採用的容忍區間可以是使用該分佈的方法的區間。
主要結果:機率圖和 p 值
機率圖顯示,繪製的點落於 Weibull 分佈配適線的沿線,表示資料服從一個 Weibull 分配。而且,適合度檢定的 p 值為 0.178,這大於顯著水準 0.05。由於無法認定資料不遵循 Weibull 分佈,因此可以使用 Weibull 分佈的區間。
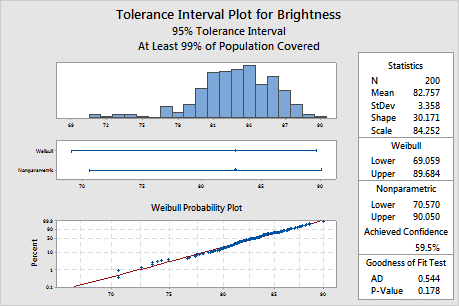
步驟 2:檢查相應方法的容忍區間
Minitab 為使用分配的方法和不假定特定分配的非參數方法提供容忍區間。您可以建立一個雙邊容忍區間,也可以建立提供上限或下限的單邊容忍區間。
雙邊 (Two-sided)
使用雙邊區間可以確定包含特定最小百分比的總體測量值的區間。
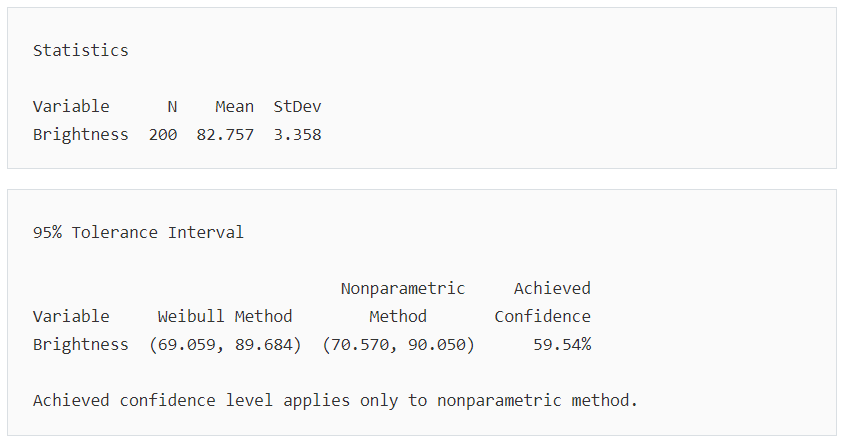
主要結果:95% 容忍區間
Weibull 區間的範圍大約為從 69.1 到 89.7,因此製造商可以具有 95% 的信心水準,對於至少 99% 所有批次的紙漿將落於此區間。對於所有批次的紙漿,平均白度水準為大約 82.8。
上限 (Upper bound)
使用上限可以確定超出特定最小百分比的總體測量值的限值。
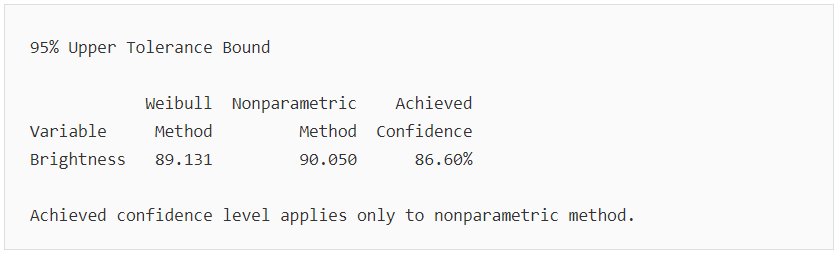
主要結果:95% 容忍上限
在此範例中,由於 Weibull 上限為 89.131,因此所有批次紙漿中至少 99% 的紙漿具有 89.131 或更低白度的信心為 95%。如果您不能假定資料服從 Weibull 分佈,請找出可配適的其他分佈或者考慮非參數上限 90.50。對於非參數方法,取得的信心為 86.60%,它遠小於目標值 95%。此結果表示,您的樣本數量太少,導致非參數方法不準確。
下限 (Lower bound)
使用下限可以確定小於特定最小百分比的總體測量值的限值。

主要結果:95% 容忍下限
在此範例中,由於 Weibull 下限為 71.105,因此所有批次紙漿中至少 99% 的紙漿具有 71.105 或更高白度的信心為 95%。如果您不能假定資料服從 Weibull 分佈,請找出可配適的其他分佈或者考慮非參數下限 70.570。對於非參數方法,取得的信心為 86.60%,它遠小於目標值 95%。此結果表示,您的樣本數量太少,導致非參數方法不準確。