- Q
-
Weibull 分配的形狀、尺度和門檻參數意指什麼?
- A
-
Weibull 分佈
Weibull 分佈是一種通用分佈,可於工程、醫學研究、品質管控、金融和氣候學中的各種應用進行建模。例如,此分佈經常與可靠性分析結合使用,以對失效時間資料 (如零件在一年、兩年或更多年之後失效的機率) 建模。Weibull 分佈也可用於對能力分析中的偏斜製程資料建模。
Weibull 分佈由形狀 (shape)、尺度 (scale) 和門檻 (threshold) 等參數所描述。門檻參數為零的情況稱為 2 參數 Weibull 分佈。僅對非負變數定義 Weibull 分佈。Weibull 分佈可以採用各種形式,具體取決於其參數的值。
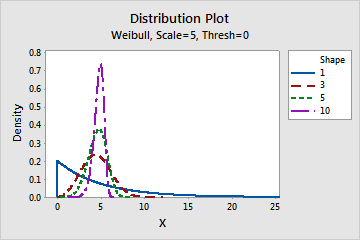
形狀參數的效果
形狀 (shape) 可描述資料的分佈情況。形狀參數為 3 近似於一條常態曲線。介於 2 和 4 之間的形狀仍近似於常態。值更低的形狀 (如 1.25) 會產生向右偏斜的曲線。值更高的形狀 (如 10) 會產生向左偏斜的曲線。
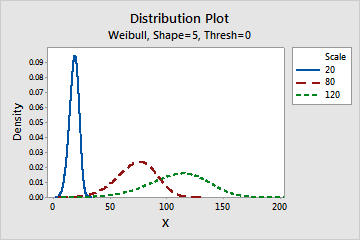
尺度參數的效果
尺度 (scale) (或特徵壽命) 是資料的第 63.2 百分位數。尺度可定義與門檻值相關的 Weibull 曲線的位置,這類似于平均值定義常態曲線的位置的方式。例如,尺度參數為 20 表示 63.2% 的設備將在門檻時間後的前 20 個小時內失效。
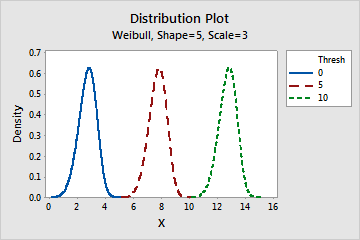
門檻參數的效果
門檻 (threshold) 是分佈偏離 0 的偏移度。負門檻參數表示分佈向 0 的左側偏移,正門檻參數表示分佈向 0 的右側偏移。所有資料必須大於門檻參數。2 參數 Weibull 分配與 3 參數 Weibull 分配相同,但門檻參數為 0。例如,2 參數 Weibull(3,100) 分配與 3 參數 Weibull(3,100,50) 分配完全相同,只是 3 參數 Weibull 分配向 0 的右側偏移了 50 個單位。
由於 Weibull 分佈可以具有其他類型分佈的特徵,因此它在配適不同類型的資料時極其靈活。例如:
• Weibull 分佈是存在偏斜資料時常態分佈的備選。
• 指數分佈是 Weibull 分佈的一種特殊情況,常用於研究輻射或風速的散佈。
• 如果 X 服從 Weibull 分佈,則 Ln(X) 服從極值分佈 (extreme value distribution)。極值 分佈用於描述極端條件,如:極端陣風、地震期間的極端能量或極端機械或物理壓力。