FAQ | Minitab

R² 是反應變數變異中由其與一個或多個預測變數的關係所解釋的百分比。一般而言，R² 越大，模型與資料配適得越好。R² 始終介於 0 與 100% 之間。R 平方也被稱為判定係數或多元判定係數 (在多元線性迴歸中)。

R 平方的圖形解釋

您可以按照配適值來繪製觀測值，以圖形方式解釋迴歸模型的 R² 值。

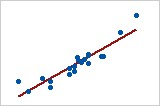
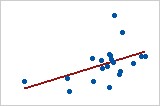
觀測值與配適值圖

第一個迴歸模型解釋 85.5% 的變異，而第二個迴歸模型解釋 22.6% 的變異。迴歸模型解釋的變異越多，資料點越接近於所配適的迴歸線。從理論上來說，如果模型可以解釋 100% 的變異，則配適值將始終等於觀測值，並因此所有數據點都將落於配適的迴歸線上。

調整的 R² 是反應變數變異中由其與一個或多個預測變數的關係所解釋的百分比，並對於模型中的預測變數個數進行了調整。由於添加新項時任何模型的 R² 總是會增大，因此這種調整很重要。模型的項越多，可能就配適得更好，原因很簡單，因為它有更多項。

使用調整的 R²，確定當您想要調整模型中的預測變數數時，模型與您資料的配適程度。調整的 R²值納入模型中的預測變數個數，以幫助您選擇正確的模型。

例如：您工作於一家洋芋片公司，該公司正在檢查影響每個包裝內碎洋芋片百分比的因素。您在迴歸模型中將馬鈴薯相對於其他成分的百分比、冷卻速度和加工溫度作為預測變數。當您以向前逐步方式添加預測變數時，您得到以下結果：

第一步產生在統計意義上顯著的迴歸模型。透過增加第二項，您看到調整的 R² 增大，這表明“冷卻速度”已改進模型。添加第三項加工溫度，而當 R² 增大時，調整的 R² 卻未增大。由於加工溫度並未改進模型，因此可以考慮將其從模型中刪除。

使用預測的 R² 可確定模型對新觀測值的反應結果的預測能力。預測的 R² 值越大，說明模型的預測能力越強。

預測的 R² 的計算過程是從資料集中系統地刪除每個觀測值、估計迴歸方程，然後確定模型對已刪除觀測值的預測能力。預測的 R² 在 0 到 100% 之間，且根據 PRESS 統計量計算得出。

預測的 R² 可以阻止過度配適模型，並且對於比較模型而言，它比調整的 R² 更有用，因為計算它時使用的是不包括在模型估計中的觀測值。過度配適是指看似可以對用於模型計算的資料集解釋預測變數與反應變數之間的關係，但無法為新觀測值提供有效預測的模型。

例如：您在一家財務諮詢公司工作，並正在開發預測未來市場情況的模型。模型看起來很有希望，因為其 R² 為 87%。但是，在計算預測的 R² 時，您會發現它下降到 52%。這可能表示過度配適模型，還說明您的模型將無法像配適現有資料一樣準確地預測新觀測值。